MICA Then & Now
‘Coding’ and Computational Modeling in Mathematics at Brock University
The 22-Year ‘MICA’ Story: Innovation, Evolution, Contribution
For over 20 years, math majors and future math teachers at Brock have been learning to use programming for pure or applied mathematics inquiries in the context of 3 project-based courses known as MICA I-II-III.
2001 marked the beginning of an exciting new direction for mathematics at Brock University: The Department of Mathematics and Statistics launched a sequence of courses known as ‘MICA’ – Mathematics Integrated with Computers and Applications – that sought to encourage mathematical creativity, develop mathematics concepts hand-in-hand with computers, and ultimately equip students with the skills needed to solve modern-day problems in research, industry, business, and education [1][2]. Such courses were at the forefront of embracing the power of computation in mathematics, described ten years later by the European Mathematical Society: “Together with theory and experimentation, a third pillar of scientific inquiry of complex systems has emerged in the form of a combination of modeling, simulation, optimization, and visualization” ([3], p. 2).


The first postcard advertisement for the MICA courses, printed in 2001.
The core of the MICA courses is project work, counting for 70–80% of students’ grades. Indeed, it’s primarily through the completion of inquiry projects (4–5 in each course) that students learn to design, program, and use interactive computer environments – so-called ‘exploratory objects’ (EOs) – to investigate mathematical concepts, conjectures, theorems, or real-world situations [4][5]. For example, a MICA I project has invited students to develop EOs for examining, numerically and graphically, the behaviour of discrete dynamical systems involving parameters; and another project, implemented in MICA II, has introduced students to building EOs for simulating and analysing battles between two opposing armies, as modelled by discrete equations [6].
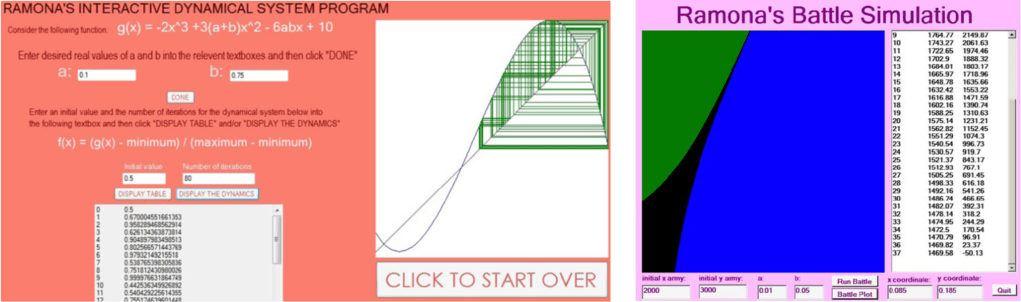
EOs for investigating discrete dynamical systems (left) and battle simulations (right), constructed as part of assigned MICA projects.
In the final project of each MICA course, students have the chance to take ownership of their inquiries, working individually or in pairs to investigate a topic of their choice ([7] provides some examples). For some students, this means constructing an EO to engage in pure or applied mathematics research: Adam, for instance, used his EO to formulate a conjecture concerning the bounded area of the function defining the Mandelbrot set, and Matthew and Kylie programmed a simulator to answer the question: “Is it better to walk or run in the rain?” Other students, often future mathematics teachers, decide instead to create a ‘learning object’ (LO): an interactive program that provides a guided learning experience of a school mathematics concept [4], such as the one created by Ramona and Cassie on perimeter. Such ‘passion projects’ can serve as important milestones on a student’s journey through the MICA courses, enabling them to demonstrate their accumulation of skills as creative problem solvers in an increasingly computational world [6].

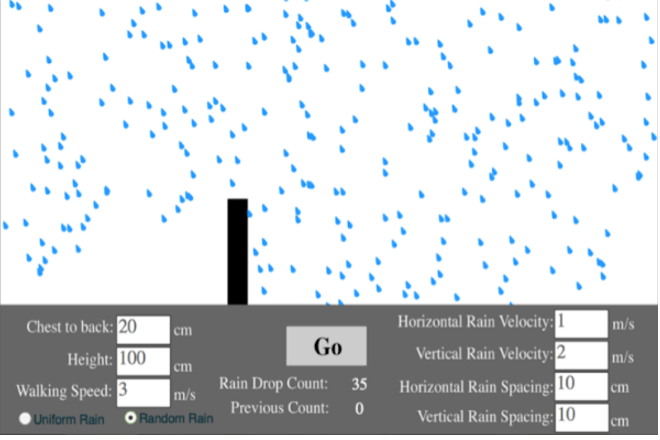
EOs for investigating the Mandelbrot Set (left) and whether it is better to walk or run in the rain (right), constructed as part of original projects in MICA II.
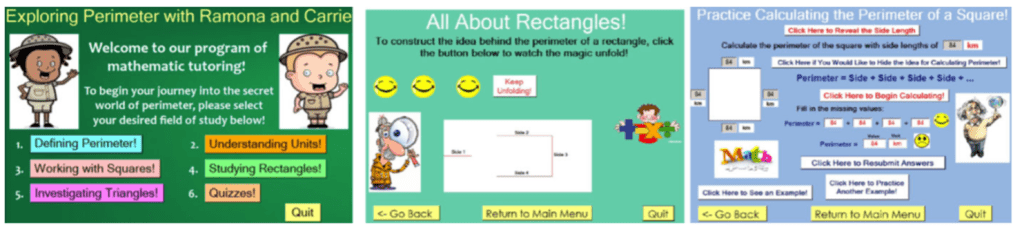
Selected parts of a LO for supporting the learning of perimeter, constructed as part of an original project in MICA I.
MICA courses have evolved over the years, including the addition of a MICA III course for future teachers which, in part, addresses the recent integration of ‘coding’ in the Ontario Gr. 1–9 math curriculum.
Even after 22 years, certain elements of the MICA courses have remained the same. To support the core – students’ project work – the courses involve two hours of weekly lectures and two hours of weekly sessions in computer labs, which are typically capped at 35 students. Lectures primarily introduce mathematical content that serves as a background and motivation for the programming-based mathematical tasks completed in labs [5]. And tasks are purposefully designed to build students’ confidence and fluency by becoming progressively more challenging: While in MICA I students focus on developing programming skills in accessible mathematical contexts, MICA II and III challenge students to code and use simulation to explore more advanced mathematics and more complex systems [8]. The following table illustrates such a progression by listing examples of topics students may encounter in their MICA course projects. Topics in MICA I have been relatively stable since 2001, whereas topics in MICA II and III have changed with time and according to 9 different instructors’ interests (see [9] for lab and project guidelines for MICA I and examples of project guidelines for MICA II and MICA III for future math teachers).
| MICA | PROJECT | TOPIC | |
| I | 1 | Conjecture about prime numbers or hailstone sequences | |
| 2 | RSA encryption method | ||
| 3 | Discrete dynamical systems (cubic with two parameters) | ||
| 4 | Original, end-of-term project, on a student-selected topic | ||
| II | 5 | Buffon needle problem and Monte Carlo integration | |
| 6 | Markov chains applied to income demographics and chronic illnesses | ||
| 7 | Dynamical system of the logistic function and bifurcation diagram | ||
| 8 | Simulation of battles (Lanchester equations) | ||
| 9 | Original, end-of-term project, on a student-selected topic | ||
| III | For math and science majors | For future math teachers | |
| 10 | Exponential growth with harvesting model and application to world population | Calendar problem in Scratch | |
| 11 | Power laws in spatial models applied to patterns on the shell of certain snail species | Simulations about Bertrand’s Paradox | |
| 12 | Determining dynamical exponents in random and ballistic deposition models | Prey-predator biological model (Lotka-Volterra) | |
| 13 | Percolation and wetting models | Randomness of DNA sequences | |
| 14 | Original, end-of-term project, on a student-selected topic | Original, end-of-term project, on a student-selected topic | |
Examples of topics encountered in the sequence of three MICA courses.
All of this said, there have been some significant changes to the MICA courses since their inception [5]. For example, in 2018, MICA III was split into two courses to serve the varying needs and interests of two student populations: math and science majors, and future math teachers. To better support the teachers, MICA III was revised to include new objectives and related activities. In addition to completing inquiry projects to further their own experience learning to use programming to investigate mathematics, the future teachers also engage in complementary reading and reflection to deepen their understanding of their experience, including the affordances of computing for mathematics learning. After the Ontario Ministry of Education made ‘coding’ an official part of the Gr. 1–9 Mathematics curricula in 2020 and 2021 [10][11], another objective was added: Building an awareness of the place of programming in the curricula and relevant teaching approaches. Key to addressing this last objective is a new kind of original end-of-term ‘passion project’ in which the future teachers collaborate with teachers in local schools to prepare and implement coding-based activities in mathematics classrooms [12][13].
The above evolutions have arisen alongside increasing support for the integration of coding and computational modelling in all levels of mathematics education. Consider, for instance, PISA’s 2021 international mathematics assessment framework [14], which has taken the following position: By the time students are 15 years old, they “should possess and be able to demonstrate computational thinking skills as they apply to mathematics as part of their problem-solving practice,” (p. 5) which means being able to engage in “defining and elaborating mathematical knowledge that can be expressed by programming” (p. 12). From being celebrated as a pioneering program of its kind in Canada back in 2001, the MICA courses are now part of a university math ed community aiming to inspire students who may have been learning to use programming for mathematical investigation since the age of 6. It will be interesting to see the kinds of evolutions this may stimulate in the future.
MICA implementation has been providing a rich context for research of different aspects of learning to use programming as a meaningful tool for mathematics learning and its teaching.
Not long after the MICA courses were launched in 2001, some faculty members involved in their design and implementation began to report on the innovative approach in educational publications and events: e.g., a presentation on MICA was a natural fit at the 2006 ICMI Study Conference seeking to revisit the terrain of digital technologies and mathematics teaching and learning [15]. Reflecting more deeply on the project work students encounter in MICA led to the development of a first theoretical model for thinking about students’ learning activity [16].
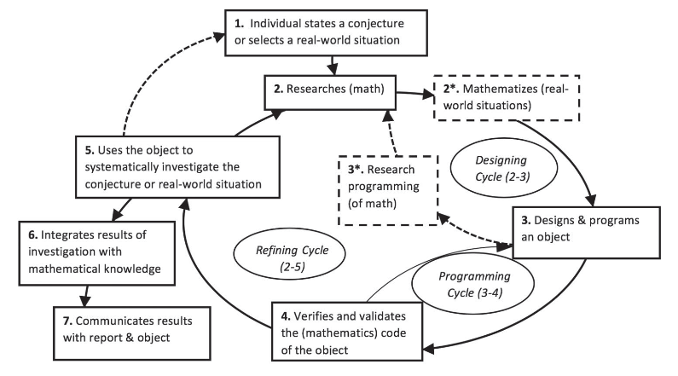
Development process model of student engagement in programming for a pure or applied mathematics inquiry project ([17], p. 1025). See [18] for a video presenting a dynamic illustration of the model in the context of two student projects.
And so the stage was set for a longer-term research project aiming to use the MICA context to better understand how students learn to use programming as a meaningful tool for university mathematics, and how instructors and universities can support that learning.
Over the past 5 years, the SSHRC-funded research project (2017–23) has involved 10 research collaborators and 13 research assistants in the exploration of various topics, which can be grouped under the following 4 foci:
- Students’ learning: e.g.,
- appropriation of programming as the development and evolution of a complex web of instrumented-action schemes, with individual and social aspects [17][19][20][21]
- constructionist experiences through 14 programming-based projects [6]
- ways of thinking, and facing and overcoming challenges in inquiry projects [22][23]
- empowerment, identity, and mindsets [24][25][26]
- contributions of an institutional approach, including the development of programming-based praxeologies [27]
- predicative and operational knowledge in a project-based approach [28]
- Instructors’ teaching: e.g.,
- roles and demands for supporting a constructionist learning environment [29][30]
- decision-making and actions for supporting students’ development of schemes [31]
- assessment of students’ computational thinking for mathematics [32]
- effective features for supporting students’ learning in a project-based approach [33]
- Task and task design: e.g.,
- Teacher education: e.g.,
As the SSHRC project is coming to an end, the team is excited to think about the kinds of topics, collaborations, and contexts that can continue to move the research forward!
References
[1] Ralph, W. (2001). Mathematics takes an exciting new direction with MICA program. Brock Teaching, 1(1), 1.
[2] Ben-El-Mechaiekh, H., Buteau, C., & Ralph, W. (2007). MICA: a novel direction in undergraduate mathematics teaching. Canadian Mathematics Society Notes, 39(6), 9–11.
[3] European Mathematical Society. (2011). Position paper of the European Mathematical Society on the European Commission’s contributions to European research.
[4] Muller, E., Buteau, C., Ralph, W., & Mgombelo, J. (2009). Learning mathematics through the design and implementation of exploratory and learning objects. International Journal for Technology in Mathematics Education, 16(2), 63–74.
[5] Buteau, C., Muller, E., & Ralph, B. (2015). Integration of programming in the undergraduate mathematics program at Brock University. In Online proceedings of the Math + Coding Symposium.
[6] Buteau, C., Muller, E., Marshall, N., Sacristán, A.I., & Mgombelo, J. (2016). Undergraduate mathematics students appropriating programming as a tool for modelling, simulation, and visualization: A case study. Digital Experiences in Mathematics Education, 2(2), 142–166.
[7] Brock University. (n.d.). MICA – Mathematics integrated with computers and applications. www.brocku.ca/mathematics/studentprojects
[8] Buteau, C., & Muller, E. (2014). Teaching roles in a technology intensive core undergraduate mathematics course. In A. Clark-Wilson, O. Robutti, & N. Sinclair (Eds.), The Mathematics Teacher in the Digital Era (pp. 163–185). Springer.
[9] CTmathU: Computational Thinking in University Mathematics. (n.d.). Teaching resources. https://ctuniversitymath.ca/category/teaching-resources/
[10] Ontario Ministry of Education. (2020). Ontario curriculum and resources: Elementary mathematics. https://www.dcp.edu.gov.on.ca/en/curriculum/elementary-mathematics
[11] Ontario Ministry of Education. (2021). Ontario curriculum and resources: Grade 9 mathematics. https://www.dcp.edu.gov.on.ca/en/curriculum/secondary-mathematics/courses/mth1w
[12] Steepe, J. (2022, May 5). Brock math students collaborate with local teachers on coding lessons. Brock News.
[13] Mathematics Knowledge Network. (n.d.). Niagara Catholic + Brock U Collaborative Coding: Collaboration Resources and Four Experience Reports. http://mkn-rcm.ca/niagara-catholic-brock-u-collaborative-coding/
[14] Organisation for Economic Cooperation and Development (OECD). (2018). PISA 2021 mathematics framework (draft).
[15] Buteau, C., & Muller, E. (2006). Evolving technologies integrated into undergraduate mathematics education. In L.H. Son, N. Sinclair, J.B. Lagrange, & C. Hoyles (Eds.), Proceedings for the Seventeenth ICMI Study Conference: Digital Technologies and Mathematics Teaching and Learning: Revisiting the Terrain. Hanoi University of Technology.
[16] Buteau, C., & Muller, E. (2010). Student development process of designing and implementing exploratory and learning objects. In V. Durand-Guerrier, S. Soury-Lavergne, & F. Arzarello (Eds.), Proceedings of CERME 6 the Sixth Congress of the European Society for Research in Mathematics Education (pp. 1111–1120).
[17] Buteau, C., Gueudet, G., Muller, E., Mgombelo, J., & Sacristán, A.I. (2019). University students turning computer programming into an instrument for “authentic” mathematical work. International Journal of Mathematical Education in Science and Technology, 57(7), 1020–1041.
[18] Balt, K., & Buteau, C. (2020, September 4). Using programming for pure/applied mathematics investigation: Mandelbrot set and running in the rain illustrations [Video]. YouTube. https://youtu.be/irTlCE-eXhc
[19] Buteau, C., Muller, E., Mgombelo, J., Sacristán, A.I., & Driese, K. (2020). Instrumental genesis stages of programming for mathematical work. Digital Experiences in Mathematics Education, 6(3), 367–390.
[20] Gueudet, G., Buteau, C., Muller, E., Mogombelo, J., Sacristán, A.I., & Santacruz Rodríguez, M. (2022). Development and evolution of instrumented schemes: a case study of learning programming for mathematical investigations. Educational Studies in Mathematics, 110, 353–377.
[21] Gueudet, G., Buteau, C., Broley, L., Mgombelo, J., Muller, E., Sacristán, A.I., & Santacruz Rodríguez, M. (2022). Understanding how students learn programming for mathematics inquiry at university: Schemes and social-individual dialectics. In J. Hodgen, E. Geraniou, G. Bolondi, & F. Ferretti (Eds.), Proceedings of CERME 12 the Twelfth Congress of the European Society for Research in Mathematics Education (pp. 2411–2418). Free University of Bozen-Bolzano, Italy and ERME.
[22] Mgombelo, J., Forbes, W., Buteau, C., Muller, E., & Sacristán, A.I. (2021, July). Students’ ways of thinking in computer-based mathematics investigation projects. 14th International Congress for Mathematics Education (ICME14), Shanghai, China.
[23] Broley, L., Buteau, C., Levay, D., Marshall, N., Muller, E., & Sardella, J. (2022). Students facing and handling challenges in programming-based mathematics inquiry projects. In S. Smith Karunakaran & A. Higgins (Eds.), Proceedings of the 24th Annual Conference on Research in Undergraduate Mathematics Education (pp. 63–71).
[24] Gannon, S. (2018). Undergraduate students’ sense of empowerment in programming-based mathematical explorations. In J. Holm & S. Mathieu-Soucy (Eds.), Proceedings of the 2018 Annual Meeting of the Canadian Mathematics Education Study Group (pp. 237–238). CMESG. View poster here.
[25] Toor, A., Mgombelo, J., & Buteau, C. (2019). Undergraduate students’ enactment of identity in programming and mathematics learning environment. In U.T. Jankvist, M. van den Heuvel-Panhuizen, & M. Veldhuis (Eds.), Proceedings of CERME 11 the Eleventh Congress of the European Society for Research in Mathematics Education (pp. 4867-4874). Freudenthal Group & Freudenthal Institute, Utrecht University, Netherlands and ERME.
[26] Forbes, W.A., Mgombelo, J., Gannon, S., & Buteau, C. (2019). Undergraduate students’ mindsets in a computer programming mathematical learning environment. In U.T. Jankvist, M. van den Heuvel-Panhuizen, & M. Veldhuis (Eds.), Proceedings of CERME 11 the Eleventh Congress of the European Society for Research in Mathematics Education (pp.1419-1426). Freudenthal Group & Freudenthal Institute, Utrecht University, Netherlands and ERME.
[27] Broley, L., Buteau, C, & Mgombelo, J. (2022). University students learning programming-based practices for mathematics inquiry: Contributions of an institutional approach. In J. Hodgen, E. Geraniou, G. Bolondi, & F. Ferretti (Eds.), Proceedings of CERME 12 the Twelfth Congress of the European Society for Research in Mathematics Education (pp. 2357–2364). Free University of Bozen-Bolzano, Italy and ERME.
[28] Broley, L., Ablorh, E., Buteau, C., Mgombelo, J., & Muller, E. (2022). Effectiveness of a project-based approach to integrating computing in mathematics. In S. Smith Karunakaran & A. Higgins (Eds.), Proceedings of the 24th Annual Conference on Research in Undergraduate Mathematics Education (pp. 72–80).
[29] Buteau, C., Sacristán, A.I., & Muller, E. (2019). Roles and demands in constructionist teaching of computational thinking in university mathematics. Constructivist Foundations, 14(3), 294–309.
[30] Sacristán, A.I., Santacruz Rodríguez, M., Buteau, C., Mgombelo, J., & Muller, E. (2020). The constructionist nature of an instructor’s instrumental orchestration of programming for mathematics, at university level. In B. Tangney, J. Rowan Byrne, & C. Girvan (Eds.), Proceedings of the 2020 Constructionism Conference (pp. 448–499).
[31] Buteau, C., Muller, E., Santacruz Rodiguez, M., Mgombelo, J., Sacristán, A.I., & Gueudet, G. (2023). Instrumental orchestration of using programming for authentic mathematics investigation projects. In A. Clark-Wilson, O. Robutti, & N. Sinclair (Eds.), The Mathematics Teacher in the Digital Era (pp 289–322). Springer.
[32] Buteau, C., & Muller, E. (2017). Assessment in undergraduate programming-based mathematics courses. DigitalExperiences in Mathematics Education, 3(2), 97–114.
[33] Broley, L., Ablorh, E., Buteau, C., Mgombelo, J., & Muller, E. (2022). Effective orchestration features of a project-based approach to learning programming for math investigation. In M. Trigueros, R. Hochmuth, & J. Peters (Eds.), Proceedings of INDRUM 2022 Fourth Conference of the International Network for Didactic Research in University Mathematics (pp. 592–601). Leibniz University Hannover and INDRUM.
[34] Broley, L., Buteau, C., & Muller, E. (2017). (Legitimate peripheral) computational thinking in mathematics. In T. Dooley, & G. Gueudet (Eds.), Proceedings of CERME 10 the Tenth Congress of the European Society for Research in Mathematics Education (pp. 2515–2522). DCU Institute of Education and ERME..
[35] Buteau, C., Muller, E., Mgombelo, J., Rafiepour, A., & Sacristán, A.I. (2018). Features of ‘authentic’ programming-based mathematical tasks. In H.-G. Weigand, A. Clark-Wilson, A. Donevska-Todorova, E. Faggiano, N. Grønbæk, & J. Trgalova (Eds.), Proceedings of MEDA the 5th ERME Topic Conference on Mathematics Education in the Digital Age (pp. 301–302). University of Copenhagen. View poster here.
[36] Mgombelo, J., Pinar Sen, A., Buteau, C., Muller, E., Sacristán, A.I., & Santacruz Rodríguez, M. (In Press). Pre-service teachers using programming to design learning objects: A case study. In J. Hodgen, E. Geraniou, G. Bolondi, & F. Ferretti (Eds.),Proceedings of CERME 12 the Twelfth Congress of the European Society for Research in Mathematics Education (pp. 3211–3218). Free University of Bozen-Bolzano, Italy and ERME.
[37] Broley, L., Buteau, C., & Muller, E. (2022). Coding in math learning: A ‘triple instrumental genesis’ approach to support the transition from university learner to school teacher. In M. Trigueros, R. Hochmuth, & J. Peters (Eds.), Proceedings of INDRUM 2022 Fourth Conference of the International Network for Didactic Research in University Mathematics (pp. 568–569). Leibniz University Hannover and INDRUM. View poster here.
[38] Sacristán, A.I., Santacruz-R., M., Buteau, C., Mgombelo, J., Muller, E. (2022). Future teachers’ appropriation of computer programming as a mathematical instrument and a resource for teaching. Proceedings of the 13th ERME Topic Conference (ETC13) on Mathematics Education in the Digital Age (MEDA3). (pp. 256-263). Nitra, Slovakia. September 2022.
Written and edited in April 2023 by Dr. Laura Broley, in collaboration with (alph. order) Dr. Chantal Buteau, Dorothy Levay, Neil Marshall, Dr. Eric Muller, and Jessica Sardella.


